Thanks

Our thanks goes to:

Fabian Kunze and Simon Hudon for participating in the problem selection.

Fabian Kunze for doing all translations to Coq.

Simon Hudon and Kevin Kappelmann for translating the problems to Lean.

Jonas Bayer, Manuel Eberl, Martin Raszyk, Daniel Ricketts, and Christoph Walther for submitting problems.

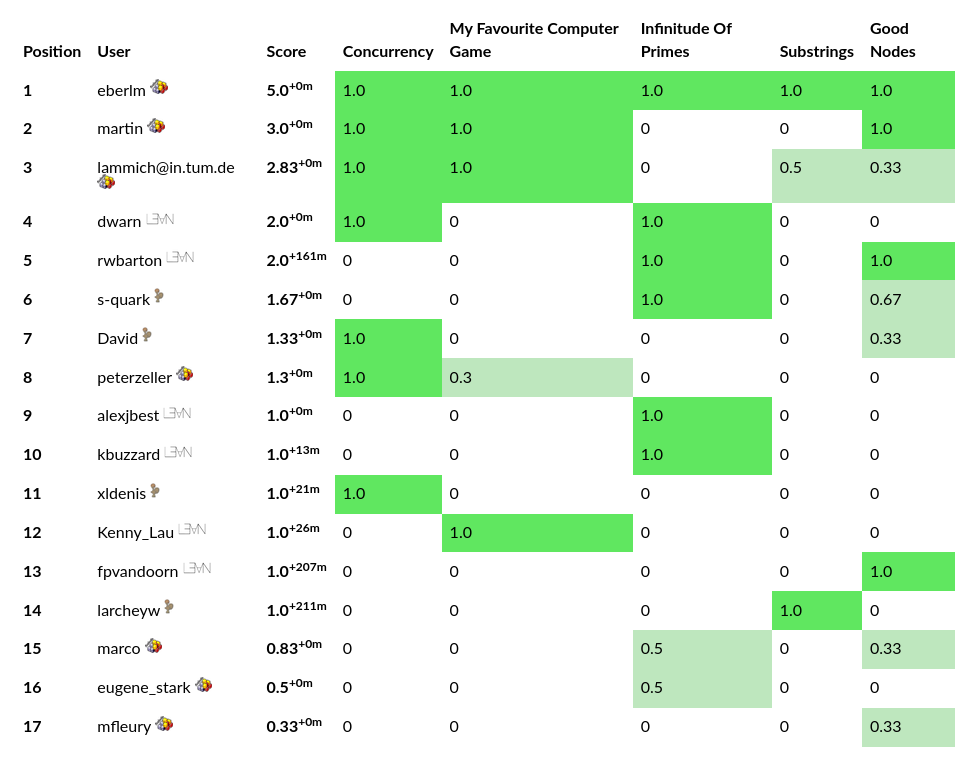
Final Leaderboard

Solutions

Github repository with solutions: https://github.com/maxhaslbeck/proofground2020-solutions

Send us a pull request with your own!

Concurrency

Submitted by: Daniel Ricketts

This problem comes from a note called "Teaching Concurrency" by
Leslie Lamport.
In this problem, there are N processes and two arrays of length N, x and y.
Each process i executes the following sequence of statements:

x[i] := 1;
y[i] := x[(i-1) mod N];

The reads and writes of each x[j] are assumed to be atomic.
This algorithm has the property that once all processes have finished, at
least one y[j] = 1.

I've written proofs of this property in a few different proof systems,
including Coq: https://github.com/dricketts/teaching-concurrency/blob/master/coq.v.
That github repository contains solutions in other systems.

Isabelle Solution

definition indinv where
  "indinv st ≡ safe st ∧ (∀i. Proc i ⟶ (pc st i = assign_y ∨ pc st i = finished) ⟶ x st i = 1)"

lemma Proc_mod :
  "∀ i. Proc i ⟶ Proc ((i + 1) mod N)"
  unfolding Proc_def by auto

lemma reachable_indinv :
  "indinv st" if "reachable st"
  using that
proof induction
  case (init init_x init_y)
  then show ?case
    using proc_0 by (auto simp: indinv_def safe_def)
next
  case (x_step st i)
  then show ?case
    by (auto simp: indinv_def safe_def update_x_def update_pc_def)
next
  case (y_step st i)
  then show ?case
    apply (auto simp: indinv_def safe_def update_y_def update_pc_def)
     apply (metis Proc_mod Suc_eq_plus1)+
    done
qed

theorem reachable_safe :
  "safe st" if "reachable st"
  using reachable_indinv[OF that] unfolding indinv_def ..

My Favorite Computer Game

Submitted by: Manuel Eberl

Infinitude Of Primes

Submitted by: Christoph Walther

Proving the infinitude of primes by pronic numbers.

Prove that
(Thm 1) ∀ n : N P(pf(S(n)+1))
(Thm 2) ∀ n, m : N pf(S(n)+1) = pf(S(m)+1) → n = m holds, where

- N denotes the non-negative integers,
- S : N → N is a mapping satisfying S(0) ≥ 2 and S(n + 1) := S(n) * (S(n) + 1),
- P(n) denotes that n is prime, and
- pf(n) stands for the smallest prime factor of n, provided n ≥ 2.

Infinitude Of Primes

Main approach for (Thm 2):

n:          0 | 1 | 2  | 3
S(n):       2 | 6 | 42 | 1806 = 42 * 43
S(n)+1:     3 | 7 | 43 | 1807
pf(S(n)+1): 3 | 7 | 43 | 13 (13 * 139 = 1807)

S(m) + 1 | S(n) if m < n

Infinitude Of Primes

Main approach for (Thm 2):

• Show that S(m) + 1 | S(n) if m < n
• Moreover, pf(S(n)) | S(n) for any n
• Let pf(S(n) + 1) = pf(S(m) + 1). Wlog, m < n:
  • S(m) + 1 | S(n)
  • hence pf(S(n) + 1) | S(n);
  • moreover, pf(S(n) + 1) | S(n) + 1;
  • but S(n) and S(n + 1) are coprime.

Substrings

Submitted by: Martin Raszyk

Originally, checker code for an ACM problem.

Only two complete solutions, one Coq, one Isabelle.

Substrings

theory Submission
  imports "HOL-Library.Sublist" Defs
begin

definition all_subseq :: "'a list ⇒ 'a list ⇒ bool" where
  "all_subseq xs ys ⟷ (∀xs'. xs' ⊑ xs ⟶ xs' ⊑ ys)"

lemma subseq_id:
  "subseq = Sublist.subseq"
  apply (intro ext)
  apply safe
  subgoal premises prems
    using prems by induction auto
  subgoal premises prems
    using prems by induction auto
    done

lemma proper_subseq_id:
  "proper_subseq = strict_subseq"
  unfolding proper_subseq_def strict_subseq_def subseq_id ..

lemmas subseq_ids = subseq_id proper_subseq_id

lemmas [termination_simp] = length_dropWhile_le

lemma subseq_empty_iff:
  "xs ⊑ [] ⟷ xs = []"
  unfolding subseq_ids by auto

lemma [simp]:
  "all_subseq [] ys ⟷ True"
  "all_subseq (x # xs) [] ⟷ False"
  unfolding all_subseq_def by (auto simp: subseq_empty_iff)

lemma [simp]:
  "all_subseq (x # xs) (y # ys) ⟷ all_subseq (x # xs) ys" if "x ≠ y"
  using that by (auto simp: all_subseq_def subseq_ids)

lemma [simp]:
  "all_subseq (x # xs) (x # ys) ⟷ all_subseq xs ys"
  apply (auto simp: all_subseq_def subseq_ids)
  by (meson subseq_Cons2 subseq_order.dual_order.trans subseq_order.order_refl)

lemma aux_correct:
  "aux xs ys ⟷ all_subseq xs ys"
  by (induction rule: aux.induct; simp)

lemma strict_subseq_ConsE:
  assumes "a # as ⊏ bs"
  obtains xs ys where "bs = xs @ a # ys" "xs ≠ []" "as ⊑ ys" | ys where "bs = a # ys" "as ⊏ ys"
  by (metis (full_types) assms list_emb_ConsD self_append_conv2 subseq_order.antisym_conv2
        subseq_order.dual_order.strict_implies_order subseq_ids)

lemma strict_subseqE:
  assumes "xs ⊏ ys"
  obtains as x bs where "ys = as @ x # bs" and "xs ⊑ as @ bs"
  using assms unfolding subseq_ids
  apply (induction xs arbitrary: ys)
  subgoal for ys
    apply (cases ys; force)
    done
  apply (erule strict_subseq_ConsE[unfolded subseq_ids])
   apply (metis append_Cons append_Nil list.exhaust list_emb_append2 subseq_Cons2_iff)
  by (metis append.simps(2) subseq_Cons2)

lemma all_proper_subseq_subdivide:
  "all_proper_subseq xs ys ⟷ (∀as x bs. xs = as @ x # bs ⟶ all_subseq (as @ bs) ys)"
unfolding all_proper_subseq_def all_subseq_def subseq_ids
  apply auto
  apply (meson list_emb_Cons not_Cons_self2 same_append_eq subseq_append_iff
          subseq_order.dual_order.order_iff_strict subseq_order.le_less_trans)
  subgoal
    by (erule strict_subseqE[unfolded subseq_ids]) auto
  done

lemma aux2_iff:
  "aux2 ys acc xs ⟷ (∀as x bs. xs = as @ x # bs ⟶ aux (acc @ as @ bs) ys)"
  apply (induction xs arbitrary: acc)
   apply auto
  subgoal
    by (smt Nil_is_append_conv append_eq_append_conv2 hd_Cons_tl hd_append2 list.sel(1) list.sel(3)
          tl_append2)
  apply force
  by (metis append_Cons)

lemma aux2_correct:
  "aux2 ys [] xs ⟷ all_proper_subseq xs ys"
  unfolding aux2_iff all_proper_subseq_subdivide aux_correct by simp

theorem judge1_correct: "judge1 xs ys ⟷ all_proper_subseq xs ys"
  unfolding judge1_def aux2_correct by auto


definition
  "judge2 xs ys ⟷ judge1 xs ys"

theorem judge2_correct:
  "judge2 xs ys ⟷ all_proper_subseq xs ys"
  unfolding judge2_def by (rule judge1_correct)

theorem judge2_is_executable:
  "judge2 ''ab'' ''ab'' ⟷ True"
  "judge2 ''ba'' ''ab'' ⟷ True"
  "judge2 ''abcd'' ''cdabc'' ⟷ False"
  by eval+

Good Nodes

Submitted by: Simon Wimmer

We expected this to be harder than substrings.

But got many good solutions.

Unfortunately, the Lean task was incorrect.